Dalam kenyataan sesungguhnya, arus kas jarang terjadi secara rapi dan terjadwal.
Fungsi standar seperti NPV mengasumsikan arus kas terjadi pada interval tetap. Namun, penerapan NPV pada arus tidak teratur dapat menghasilkan perhitungan yang meleset dari kondisi sebenarnya.
XNPV menjadi alternatif penting bagi NPV karena menghitung nilai saat ini (present value) berdasarkan tanggal sesungguhnya dari setiap arus kas, sehingga hasilnya lebih akurat dan mencerminkan nilai waktu uang lebih realistis.
File: fungsi-xnpv-excel.xlsx
Apa Itu XNPV?
XNPV adalah versi lebih akurat dari fungsi NPV di Excel karena menghitung nilai sekarang berdasarkan tanggal kapan setiap arus kas terjadi, bukan berdasarkan interval tetap.
XNPV berguna ketika:
- Arus kas tidak terjadi secara berkala,
- Tanggal pembayaran tidak teratur,
- Investasi memiliki top‑up atau pendapatan tidak terjadwal.
Singkatnya, gunakan XNPV ketika arus kas tidak rapi, tidak teratur, atau terjadi pada tanggal yang berbeda‑beda.
Kapan Menggunakan Fungsi XNPV?
Berikut kegunaan umum XNPV, tapi tidak terbatas pada:
- Investasi properti
- Proyek UMKM
- Pendanaan startup
- Pembayaran vendor yang tidak terjadwal
- Investasi dengan top-up tidak teratur
Sintak Fungsi XNPV di Excel
Sintak
XNPV(rate; values; dates)
Keterangan:
- rate (wajib): Tingkat diskonto (discount rate) per tahun.
- values (wajib): Daftar arus kas (cash flow), dimulai dari investasi awal (biasanya negatif).
- dates (wajib): Tanggal masing-masing arus kas. Jumlahnya harus sama dengan values.
Catatan Penting Saat Menggunakan Rumus XNPV
- XNPV membutuhkan setidaknya satu arus kas negatif dan satu positif.
- Tanggal harus valid dan dapat dikenali Excel.
Mengapa XNPV Lebih Akurat daripada NPV?
NPV standar mengasumsikan arus kas terjadi pada interval tetap, misalnya setiap tahun. Pada prakteknya:
- Pendapatan bisa datang lebih cepat atau lambat,
- Pembayaran bisa tidak terjadwal,
- Top-up dilakukan tidak teratur.
XNPV memperbaikinya dengan:
- menghitung berdasarkan selisih hari yang sebenarnya,
- tidak mengasumsikan periode tetap
Contoh Rumus XNPV di Excel
Menghitung XNPV dari Investasi Properti
Andi membeli kios seharga Rp 300.000.000 dan menyewakannya dengan harga dan waktu seperti tabel di bawah. Tingkat diskonto adalah 10%.
Berapakah nilai saat ini dari seluruh arus kas?
| Tanggal | Arus Kas |
| 01/01/2024 | -300.000.000 |
| 15/06/2024 | 25.000.000 |
| 10/12/2024 | 30.000.000 |
| 05/05/2025 | 35.000.000 |
| 20/11/2025 | 40.000.000 |
=XNPV(B1; B4:B8; A4:A8)Nilai saat ini dari seluruh arus kas adalah -184.427.762.
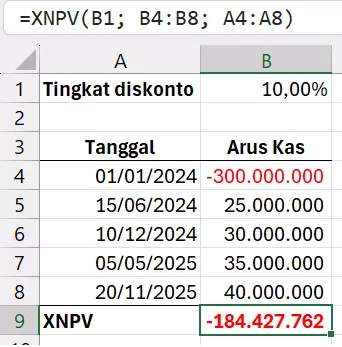
Arti nilai negatif dari hasil rumus:
- Investasi tersebut tidak layak secara finansial dengan tingkat diskonto digunakan.
- Andi kehilangan nilai ketika arus kas masa depan disesuaikan dengan waktu dan risiko.
Investasi dengan Top-Up Tidak Teratur
Andi menanam modal sebesar Rp 10.000.000 dengan arus kas lanjutan pada tanggal-tanggal berbeda seperti pada tabel berikut. Dengan tingkat diskonto 10%, berapakah nilai saat ini dari seluruh arus kas?
| Tanggal | Arus Kas |
| 01/01/2023 | -10.000.000 |
| 10/03/2023 | -5.000.000 |
| 25/08/2023 | -3.000.000 |
| 15/02/2024 | 22.000.000 |
=XNPV(B1; B4:B7; A4:A7)Rumus mengembalikan 1.686.741.

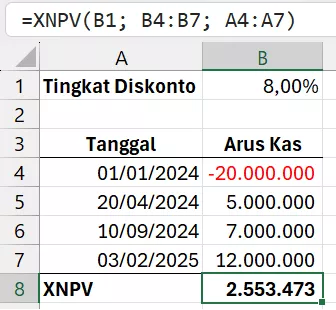
Proyek UMKM dengan Pembayaran Tidak Terjadwal
Sebuah usaha UMKM membeli peralatan penunjang produksi sebesar Rp 20.000.000. UMKM melihat arus kas masuk setelahnya pada beberapa tanggal seperti terlihat di bawah. Dengan bunga diskonto sebesar 8%, berapakah nilai bersih saat ini dari seluruh arus kas yang terjadi?
| Tanggal | Arus Kas |
| 01/01/2024 | -20.000.000 |
| 20/04/2024 | 5.000.000 |
| 10/09/2024 | 7.000.000 |
| 03/02/2025 | 12.000.000 |
=XNPV(B1; B4:B7; A4:A7)Rumus mengembalikan 2.553.473.
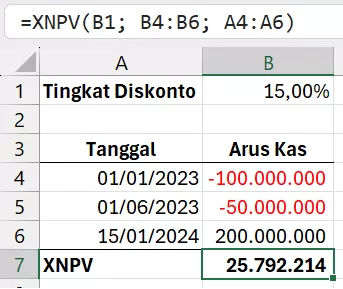
Pendanaan Startup
Andi adalah seorang investor yang menanam modal pada sebuah usaha rintisan lewat beberapa tahap pendanaan, seperti terlihat pada tabel berikut. Dengan tingkat diskonto sebesar 15%, kita dapat menentukan nilai tunai saat ini dari seluruh arus kas yang terjadi.
| Tanggal | Arus Kas |
| 01/01/2023 | -100.000.000 |
| 01/06/2023 | -50.000.000 |
| 15/01/2024 | 200.000.000 |
=XNPV(B1; B4:B6; A4:A6)Rumus XNPV mengembalikan hasil sebesar 25.792.214, yaitu besaran nilai tunai saat ini dari seluruh arus kas yang ada.
Kesalahan Umum Saat Menggunakan XNPV
| Masalah | Penyebab | Solusi |
| Error #NUM! | Data tidak sejajar | Samakan jumlah baris values dan dates |
| Error #NUM! | Tidak ada investasi awal | Tambahkan arus kas keluar pertama |
| Tanggal tidak berurutan | Data tidak disusun dengan benar | Urutkan tanggal dari paling awal |
| Menggunakan NPV untuk arus kas tidak teratur | Salah fungsi | Gunakan XNPV untuk tanggal asli |
| Tingkat diskonto salah periode | Diskonto tidak sesuai konteks | Gunakan diskonto tahunan untuk XNPV |
Perbandingan XNPV vs NPV vs XIRR
| Fungsi | Kegunaan | Kelebihan | Kekurangan |
| NPV | Menghitung nilai sekarang dengan interval tetap | Mudah digunakan | Tidak akurat untuk tanggal tidak beraturan |
| XNPV | Menghitung nilai sekarang dengan tanggal asli | Sangat akurat | Perlu tanggal lengkap |
| XIRR | Menghitung tingkat pengembalian dengan tanggal asli | Menghasilkan tingkat pengembalian | Tidak menghitung nilai sekarang |
Kesimpulan
Fungsi XNPV adalah alat untuk menghitung nilai sekarang dari arus kas yang tidak terjadi pada interval tetap. Dengan menggunakan tanggal kapan arus kas terjadi, XNPV memberikan hasil yang lebih akurat dibanding NPV standar, terutama untuk investasi properti, UMKM, startup, dan aset dengan transaksi tidak teratur.
Untuk menilai kelayakan investasi secara realistis dan sesuai kondisi dunia nyata, XNPV adalah fungsi yang wajib dikuasai.